IK ( Inverse Kinematics )ってご存知でしょうか?
引用すると、
キャラクターなどの3DCGモデルを動かすためのスケルトン構造を制御する方法の1つ。IKでは、最初にスケルトンの末端にあるジョイントの位置を設定し、そこに至るジョイントの角度を自動的に計算する。他の方法としてFK(Forward Kinematics)がある。表現したい動きに応じて、IKとFKを使い分けると良い。
って感じです。
メリットとしては、先に手の位置を決めた後に、肘や肩の位置を決められることなどです。
やってみるとわかると思うのですが、「肩→肘→手」みたいな順番で動かしていくと、なかなか思い通りの姿勢になりません。
IKの実装について解説しているサイトがあまり見つからなかったので、今回はそんなIKについて説明していこうと思います。
IK理論
今回の理論部分を簡単に説明します。
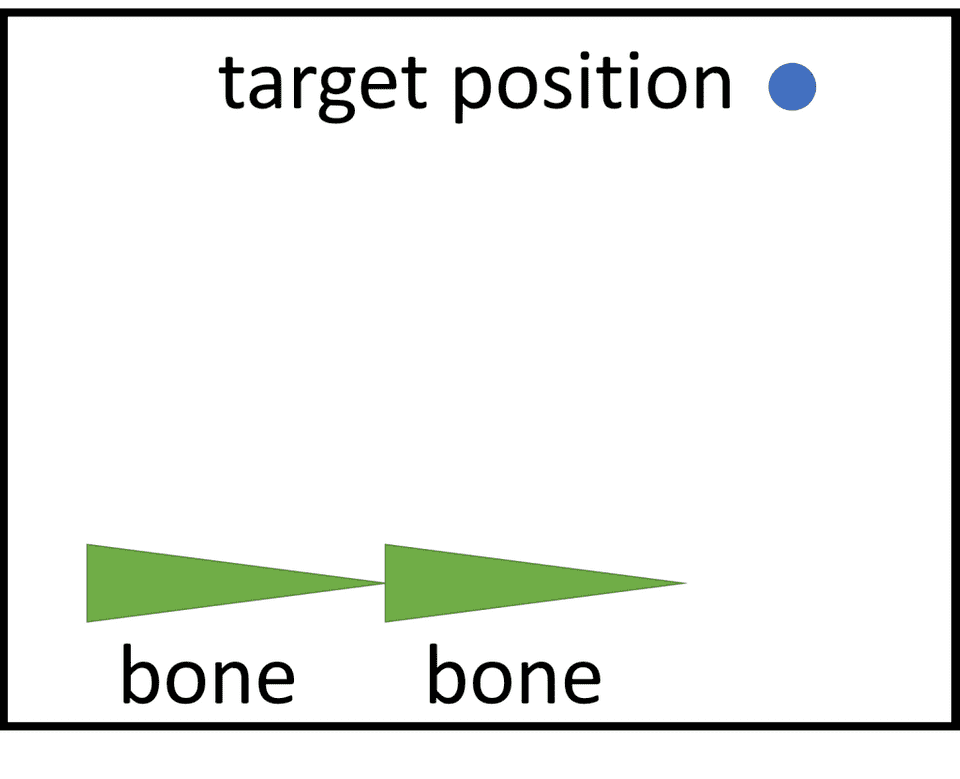
まずこんな感じで、2つの連結したボーンとIKの目的座標があるとします。
先端側のボーンを目的座標に向くように回転させます。
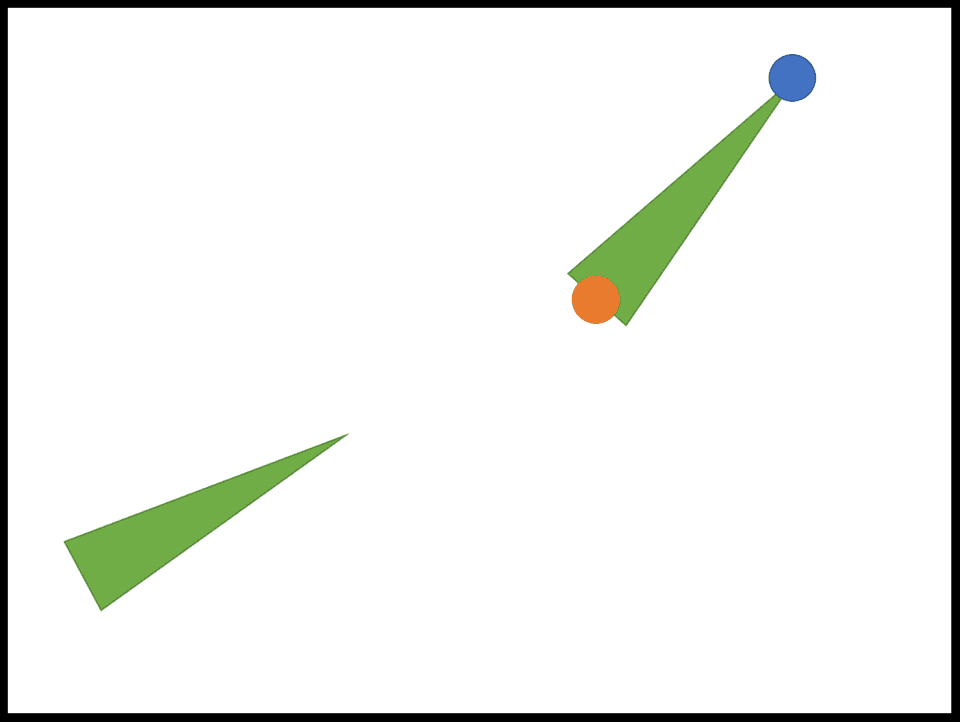
次に先端側のボーンの先端が目的座標と重なるように移動します。
先端側のボーンの根元を次の目的座標とします。
(ここではオレンジで示す新たな目的座標が求まればいい)
根元のボーンを新たな目的座標を向くように回転させます。
ボーン同士が連結するようにします。
上の手順を繰り返していくと、下の図のように2つのボーンが目的座標の方向を向くように変更されます。
任意の方向へ回転させる理論
必要なのは、習っても使わない代名詞である外積と内積です。
あとはQuaternion(クォータニオン)も必要です。
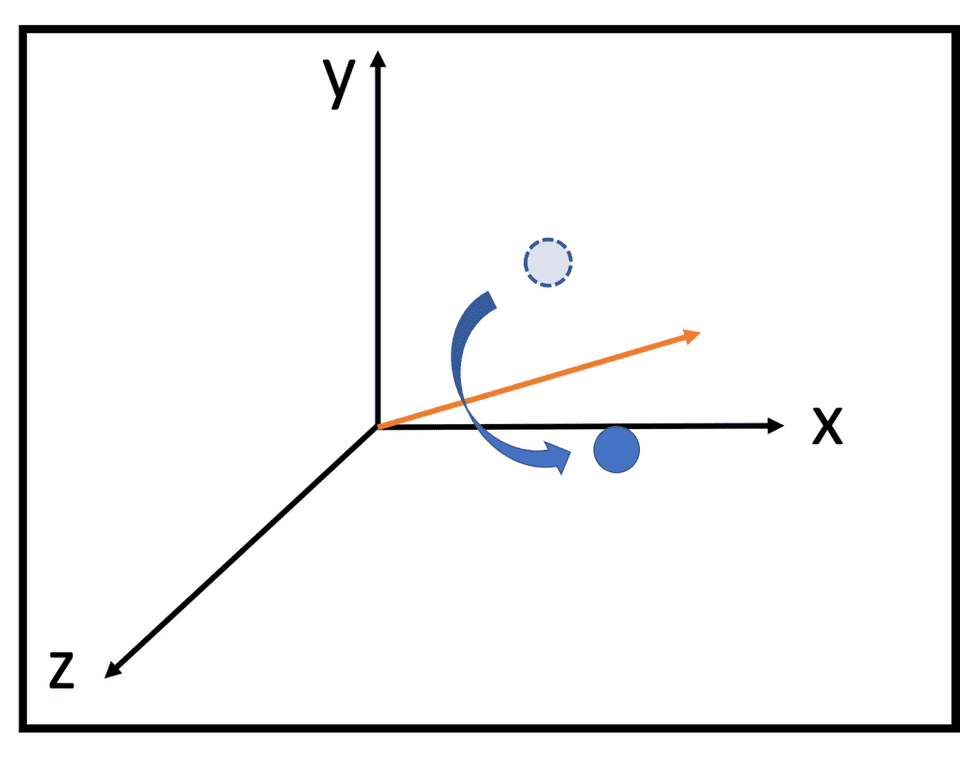
Quaternionとは回転軸(3次元ベクトル)と回転角度(スカラー)を合わせた4次元ベクトルで、回転を表すことができます。
下の図がわかりにくくて申し訳ないですが、軸が( 3, 1, 0 )で回転角が180度の時はこんな感じです。
これによってボーンを簡単に回転させることができます。
つまり、回転軸と回転角度がわかればいいわけです。
回転軸を求めるには外積を用います(Three.jsには外積を求める関数があるので使いましょう)。
外積についてはこちらのサイトがわかりやすいです。
https://atarimae.biz/archives/23716
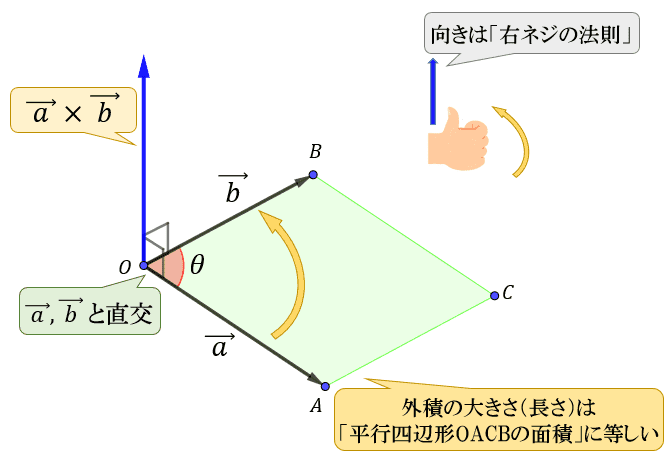
外積は下の図のような感じです。
引用: 外積とは何か。ベクトルの外積の定義・意味・大きさについて https://atarimae.biz/archives/23716
この図でいうと、IKの目的座標の動く前と動いた後をそれぞれAとBにする感じです。
それによって、回転軸を得られます。
注意点ですが、回転角が0度と180度(360度も)の時は緑の部分の面積が0になってしまうので、軸のベクトルの長さも0になってしまいます。
この時は例外処理を入れて、回転軸が0ベクトルにならないようにしなければなりません。
次に回転角を求めます。
これには内積を用います。
2つのベクトルの内積を式変形するとベクトル間の角度を用いることができます。
角度制限
角度制限を付けたいと思います。
現状の実装だと、腕がねじ切れたり、肩がぐるんぐるん回ってておかしいですから。
角度制限は Quaternionでは指定しにくいので、 オイラー角というものを使います。
オイラー角はQuaternionのように回転の表現方法の1つです。
詳しく説明しませんが、XYZのそれぞれの軸で順に回転させることで回転を表現します。 この時、XYZの順番は入れ替わることがあります。 回転させる順に「ヘディング、ピッチ、バンク」 もしくは 「ロール、ピッチ、ヨー」といいます。
(例:Y軸で30度回転させた後、 X軸で20度回転させ、 Z軸で30度回転させる。 この時ロールがY軸回転、ピッチがX軸回転、ヨーがZ軸回転です。 )
オイラー角には問題がいくつかあって、ジンバルロックが存在するのと、1つの角度を表現するのに複数のオイラー角が存在してしまうことです。
ジンバルロックは多くのサイトで解説されているので、ここでは説明しません。 こちらのサイトがわかりやすいと思います。 http://el-ement.com/blog/2018/05/19/euler-angles/
ここでは 1つの角度を表現するのに複数のオイラー角が存在 してしまうことの対策について説明します。 例えば
45度右へヘディングし90度ピッチを下げると、これは、90度ピッチを下げてから45度バンクしたのと同じです。
引用:実例で学ぶゲーム3D数学 O’REILLY 松田晃一 Fletcber Dunn Ian Parberry
これを避けるために、-180≦ヘディング ≦180、-90≦ピッチ≦90、-180≦バンク≦180 とします。
これによってオイラー角の3つ組を正準集合としました(1つの回転を示すオイラー角が1つに限定されたという意味でいいはず)。
余談ですが、ピッチが-90度または90度の時、バンクは0度になります。
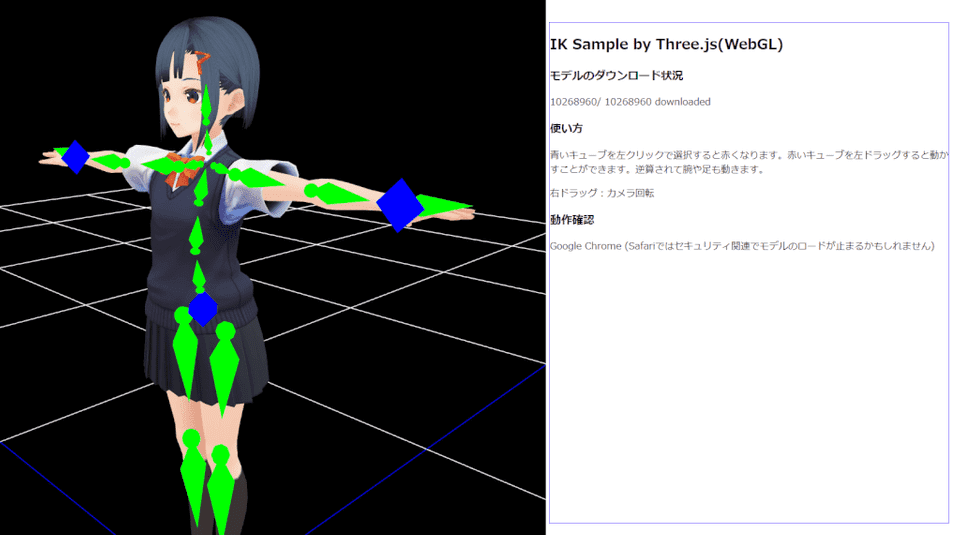
デモ
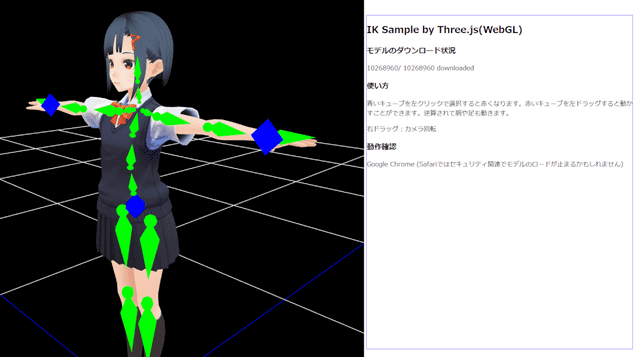
https://yosipy.github.io/Threejs_IK_Sample/
とりあえず、Chromeで簡単に動作確認しています。
角度制御によって、ある程度うまく動いているのが確認できます。
しかし、関節の構造は単純なものではなく、角度制限だけでは限界がありそうです。
かなり調整が難しいですし、姿勢によっては不安定になってしまいます。。。
結論
もし、ゲームが作りたいのであればUnityを使いましょう。
きっと幸せになれるはずです。